Mountainous regions represent 25% of Earth’s land surface and are rich in biodiversity, owing in part to their steep climatic gradients and complex topography1,2. The assumption that mountain species are responding faster to anthropogenic climate change through rapid upward range shifts leading to potential mountaintop extinctions has attracted extensive research3,4,7,8,9. Whether species are closely tracking the rate of climate warming is assessed chiefly by comparing the velocities of species range shifts with the velocities of climate change; that is, the rates at which isotherms move through the geographical space3,4,10,11,12. Past studies that assessed climate velocities have focused mainly on horizontal velocities, in km per year; that is, how fast isotherms are moving along the latitudinal and longitudinal clines of the horizontal plane (see the seminal work from Loarie et al.12 for terrestrial systems; this was then applied to marine systems by Burrows et al.13). Because isotherms are located closer to one another in mountainous regions, horizontal velocities of isotherm shifts are much slower and potentially omnidirectional in mountains, whereas they are much faster and oriented mainly poleward in the lowlands13. However, we know that climate warming also causes terrestrial species to shift along mountain slopes and thus not only horizontally but also ‘vertically’ when projected along elevation gradients—moving at very different speeds (usually expressed in m per year), and mainly upward but sometimes downward3,14,15. Despite this knowledge, global maps of the velocities of isotherm shifts projected along the vertical dimension of elevational clines in mountain regions still do not exist. This shortfall stems partly from the complex topography and the scarcity of weather stations in most mountain ranges globally5,16, which makes it difficult to accurately measure vertical velocities of climate change in mountain regions worldwide. Therefore, it is still an open question whether mountain species better track isotherm shifts vertically in elevation rather than horizontally in latitude.
Because we still lack global maps of the velocities at which isotherms are shifting vertically along elevation gradients as the climate warms, most local studies compute a rough estimate of this vertical projection of climate velocities by relying on a constant lapse rate of temperature (LRT). The LRT is defined here along mountain slopes as the normalized temperature difference at approximately 2 m above ground level between a low-elevation and a high-elevation weather station and thus it differs from a sensu stricto vertical lapse rate measured above a single geographical position. According to the laws of thermodynamics6, the LRT is 9.8 °C per km in the case of dry air1,6. Nonetheless, given that Earth’s atmosphere is not entirely dry, the LRT experienced by terrestrial organisms in reality will be less steep than 9.8 °C per km. Because of that, most studies that have compared the observed velocities of species range shifts along elevation gradients with the velocities of climate change inside a given mountain range inferred the vertical shift of isotherms by relying on a constant rate of 5.5 °C per km for the LRT11—a constant that is borrowed from limited ground observations concentrated in Europe7,17. Using this fixed rate, one can assume that if the temperature increases by 1 °C over a given period of time, then it is expected that isotherms will move upslope by about 181.8 m during that same period, which gives a vertical velocity that varies depending only on the magnitude of temperature change per unit of time. However, the LRT is not constant and varies across elevation gradients among mountain ranges as well as within a single mountain range18,19,20,21. For instance, by using long-term climatology (30-year means) from 269 weather stations in northern Italy, 205 in the Tyrol area and 166 in the Trentin–upper Adige region, covering a wide range of elevations, one study21 found that the annual mean of the LRT ranges between 5.4 and 5.8 °C per km in the Alps. In the southeastern Tibetan Plateau, the LRT was estimated22 to reach 8.5 °C per km. This large variation in the LRT partly stems from water vapour pressure because if the air condenses moisture as it cools—for example, in cloud forests—it gains some heat from condensation, which slows the cooling rate. Thus, moisture and surface temperature generate spatial variability in the LRT and consequently also generate spatial variation in the velocities at which isotherms may shift along mountain slopes as the climate warms by a given amount of temperature increase. Assessing mountain climate velocities by explicitly considering the determinants of the LRT is a crucial step in improving our understanding of species range shifts under anthropogenic climate change. Here, instead of relying on a constant LRT value of 5.5 °C per km in the Alps or of 8.5 °C per km in the Himalayas, we propose two different methods to map the spatial variation in the LRT, and we generate more meaningful estimates of the vertical velocities of isotherm shifts in mountain systems worldwide. First, we use satellite observations of land surface temperatures at fine spatial resolution to compute a satellite-derived version of the LRT (SLRT), based on local slope estimates of the relationship between temperature and elevation (Fig. 1a and Extended Data Fig. 1); and second, we use a more mechanistic approach based on the moist adiabatic LRT (MALRT), building on the laws of thermodynamics6 (Fig. 1c and Extended Data Fig. 2a,b). By combining information on the spatial variation of the SLRT and the MALRT at relatively fine spatial resolution worldwide with data on the magnitude of temperature change over time per spatial unit, we then compute maps of the vertical velocities of isotherm shifts in mountain systems: one that is based on satellite observations (SLRT); and one that mechanistically accounts for water vapour pressure conditions (MALRT). These two global maps of the vertical velocities of isotherm shifts in mountain regions are also compared to a third naive map that is based on a constant LRT of 5.5 °C per km. By using these global velocity maps, we subsequently identify the mountain regions with the highest vertical velocities of isotherm shifts in the world, and we quantify the variation in velocity values along several elevation gradients worldwide. Finally, we relate those vertical velocities of isotherm shifts, in m per year, to empirical observations of species range shifts, also in m per year, along several elevation gradients in mountain systems worldwide.
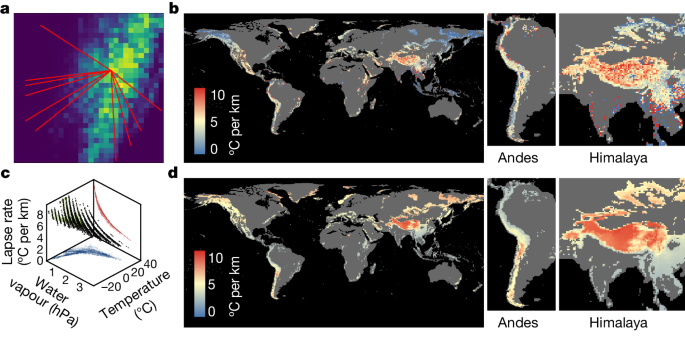
a, An example mountain range in Taiwan with a series of elevation transects, in red, defined by the highest peak at one end of the gradients and several foothills and valleys at the other end of the gradients. The background raster layer depicts the mean elevation (in m above sea level) for each spatial unit of 0.05° (around 5 km at the equator) resolution. Details can be found in the Methods and in Extended Data Fig. 1. b, Global map of the SLRT, generated at 0.5° (around 50 km at the equator) resolution across all mountain regions worldwide (except Antarctica) using satellite observations from 2011–2020. c, Three-dimensional plot showing the effect of mean annual temperature and mean annual water vapour pressure on the absolute magnitude of the MALRT (in °C per km). d, Global map of MALRT, generated at 50-km resolution across all mountain regions worldwide (except Antarctica) using climatic data from 2011–2020. Note that the colour scheme does not show the full range of data to prevent highly skewed visualization driven by extreme outliers.
Source Data
We found that there was very large spatial variation when mapping the lapse rate at a global extent (Fig. 1), either from satellite observations (SLRT; Fig. 1b) or from the laws of thermodynamics (MARLT; Fig. 1d), with values ranging (at the 5th and 95th percentiles) from −5.14 to 8.45 °C per km and from 2.94 to 8.09 °C per km, respectively. Although the two global maps show a certain degree of spatial agreement (Supplementary Results), the SLRT shows much shallower lapse rates than does the MALRT in mountain regions that are located at higher latitudes, such as in northeastern Siberia, Alaska and northwestern Canada (Fig. 1b,d). The mountain regions showing the steepest lapse rates are located in the Himalayas, with values that are very consistent with the values recently reported for the southeastern Tibetan Plateau, which range between the values of free-air dry (10 °C per km) and moist (6.5 °C per km) adiabatic lapse rates22. For comparison purposes and external validation, we also extracted data from the Global Historical Climatology Network23, focusing on empirical field data recorded by weather stations situated in mountain regions worldwide. We manage to obtain temperature lapse rates from 144 weather stations (station-based LRT; see Methods) across a total of 48 mountain sites from 2011 to 2019 (Extended Data Fig. 3a). This validation exercise confirms that there are very few mountain regions worldwide in which the network of weather stations is dense enough along mountain slopes (n > 2) to compute the LRT. Nevertheless, we found a positive relationship between the station-based LRT calculated from these very limited networks of weather-station data and our computations of the MALRT (linear regression, F1, 46 = 5.54, p = 0.02, R2 = 0.108, n = 48, Extended Data Fig. 3a). By contrast, the relationship between the SLRT and the station-based LRT did not reach statistical significance (linear regression, F1,46 = 0.774, P = 0.38, R2 = 0.017, n = 48; Extended Data Fig. 3b). Owing to the relative scarcity of weather-station data and the fact that these data are concentrated mainly in North America and Europe, our subsequent analyses will focus solely on our computations of the MALRT and the SLRT.
After combining maps of the spatial variation in the LRT with data on the rate of temporal changes in mean annual temperature (Extended Data Fig. 2c), we found notable differences in the vertical velocities (in m per year) of isotherm shifts depending on the approach we used (Fig. 2), with the constant LRT-based and MALRT-based estimates generally yielding conservative climate velocities and the SLRT-based climate velocities showing the greatest variability. Velocity values for the SLRT-based map ranged from highly negative (−26.01 m per year; at the 5th percentile) to highly positive (34.08 m per year; 95th percentile) (Fig. 2g–i). By contrast, the MALRT-based map shows velocity values ranging (at the 5th and 95th percentile) from 1.81 m per year to 10.83 m per year. When we combined the SLRT-based velocity map with the MALRT-based velocity map to reach a consensus map on the mountain regions most threatened by climate change (Methods and Fig. 3a,b), we found that 32% of the surface area covered by mountains worldwide, Antarctica excluded, is exposed to high vertical velocities of isotherm shifts that exceed the 80th percentile by either the MALRT (80th percentile: 8.25 m per year; Fig. 3) or the SLRT (80th percentile: 11.67 m per year; Fig. 3). We delineated 17 mountain regions that are partly exposed to high vertical velocities, including those in the Alaska–Yukon region, western America and Mexico, Appalachia, the Brazilian highlands, Greenland, Scandinavia, the Mediterranean basin, southern Africa, the Ural mountains, the Iran–Pakistan region, the Putorana mountains, Mongolia, northern Sumatra, the Kodar mountains, Yakutiya, northeast Asia and Kamchatka (Fig. 3c and Supplementary Data 1). Intuitively, higher rates of warming lead to higher vertical velocities of isotherms shifting faster along elevation gradients. This is the case chiefly in dry regions with a low water vapour pressure, such as Greenland, the Putorana Plateau in northern Siberia, Kamchatka, Mongolia and the Alaska–Yukon region—owing probably to the limited heat capacity of these arid areas24,25 (Fig. 3d). In addition, by relying on laws of thermodynamics, we can also anticipate that regions with higher surface temperatures and/or higher water vapour pressure might also generate high vertical velocities because of shallower lapse rates: isotherms will shift faster along such elevation gradients for the same amount of temperature change over time. Notably, these regions are not necessarily those showing significant surface warming over time. For instance, northern Sumatra, the Brazilian highlands, southern Africa and Iran–Pakistan are typical representatives of such shallow lapse rates with little surface temperature increase (Fig. 3c,d). These are mountain regions threatened by high vertical velocities of isotherm shifts that have been difficult to detect in the past by surface temperature change alone, and thus are particularly worthy of further investigation.
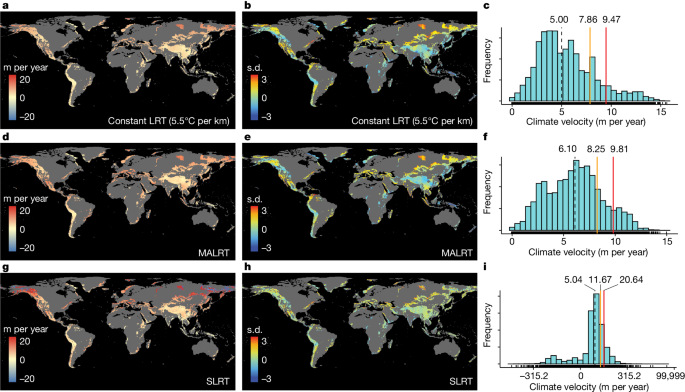
a–i, Vertical velocities of isotherm shifts (m per year) in mountain regions worldwide using a constant LRT (a–c), the MALRT (d–f) or the SLRT (g–i) (1971–1980 versus 2011–2020). b,e,h, Normalized value from the corresponding panel (a,d,g) to show clear spatial variation in each panel. c,f,i, Histograms of the velocity values across all mountain regions for the constant LRT, the SLRT or the MARLT, respectively. Note the log10 scale for the histogram displaying the range of velocity values for the SLRT. The SLRT values were rescaled using the function sign(x) × log10(abs(x) + 1) to ensure that the shifting direction is preserved and to avoid interference from the value range of logarithmic transformation. Black dashed lines indicate the median; yellow solid lines show the 80% quantile; red solid lines show the 90% quantile. The corresponding values are labelled above. Note that the colour scheme does not show the full range of data to prevent highly skewed visualization driven by extreme outliers.
Source Data
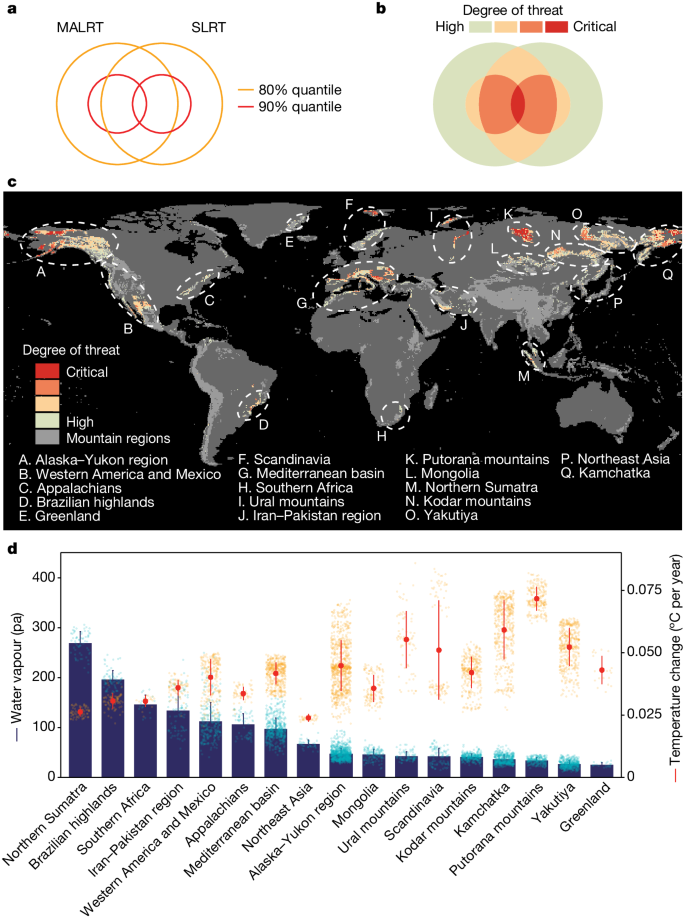
Consensus map of the vertical velocities of isotherm shifts as estimated from the SLRT or from the MALRT (see Fig. 2). a–c, Mountain regions in which velocities are greater than the 80% quantile (that is, retaining 20%) in the calculation of either the MALRT or the SLRT are labelled as critically threatened (a,b) and displayed in red (c). d, Orange points and segments represent the mean annual temperature change between the periods 1971–1980 and 2011–2020; blue bars represent the mean water vapour pressure during 2011–2020 for each of the 17 mountain regions affected by relatively fast vertical velocities of isotherm shifts. Error bars represent s.d. See Supplementary Data 1 and ‘Data availability’ for a comprehensive breakdown for each region, including sample size information. Considering that near-zero SLRT values result in extremely high climate velocity, we removed 1% outliers that are close to zero in c. Data with alternative levels of outlier removal (0.5%, 2% and 5%) are shown in Supplementary Fig. 2. Supplementary Data 3 provides a high-resolution map.
Source Data
We further compared the effects of high warming rates and steep temperature lapse rates, which act as compensatory effects on climate velocities, between arid and more humid regions. We found that in arid mountain regions with a low water vapour pressure, the temperature lapse rate accounts for 3.6% of the observed variation in climate velocity, whereas changes in surface temperature account for 96.4% of the observed variation, on the basis of the random forest analysis we performed. A detailed analysis using the Shapley value further revealed that steeper lapse rates have a smaller negative effect on climate velocities compared with higher warming rates, which increase climate velocities (Extended Data Fig. 4a). In humid regions, the temperature lapse rate accounts for 11.32% of the observed variation in climatic velocity, whereas changes in surface temperature explain 88.68% of the observed variation, on the basis of the random forest analysis we performed. The Shapley value analysis showed that steeper lapse rates still have a smaller negative effect on climate velocities than do higher warming rates (Extended Data Fig. 4b). Of note, the explanatory power of the lapse rate in wet mountains is nearly four times higher than it is in arid mountains. This difference is likely to be due to the lower magnitude of the surface temperature increase in wetter mountains (Extended Data Fig. 4c,d). Although the explanatory power of the lapse rate is, in general, relatively much lower than that of the warming rate, the striking differences that we found between arid and humid regions, in terms of the relative importance, affects the spatial variation that we report in the vertical velocity of isotherm shifts.
Focusing on the MALRT-based velocity map, we found a complex pattern of elevation-dependent velocities for isotherm shifts (also known as climate velocities; Fig. 4), with the highest vertical velocities of isotherm shifts being concentrated at low elevations. This was especially the case in the Northern Hemisphere and at a latitude of 20–30° S in the Southern Hemisphere, whereas the lowest vertical velocities were located at high elevations in the Himalayas and the Andes. Statistical results indicate that isotherm velocities are significantly higher at lower elevations (slope: −0.285 m per year∙km, degrees of freedom (df) = 12,028, t = −4.243, P < 0.001) and higher absolute latitudes (slope: 0.048 m per year∙deg, df = 12,028, t = 24.163, P < 0.001) in the Northern Hemisphere, whereas the magnitude of the effect significantly changed in the Southern Hemisphere (P < 0.001 for all interaction terms composed of elevation, latitude and hemisphere; see Methods). In the Southern Hemisphere, the elevational effect is stronger with a more negative slope estimate (slope: −1.178 m per year∙km), but the latitudinal effect was completely reversed compared with the Northern Hemisphere (slope: −0.040 m per year∙deg). The reversed latitudinal effect we detected here is likely to be due to the reduction of land area towards higher absolute latitudes in the Southern Hemisphere, where oceans predominate over landmasses, leading to a relatively higher water vapour pressure (Extended Data Fig. 2b) and consequently a lower temperature rate (Extended Data Fig. 2c). We further analysed the effects of changes in surface temperature and the MALRT on the rates of isotherm shift with elevation (Supplementary Fig. 1). We found no significant linear correlation between the rate of surface temperature change and elevation when the effect of latitude was statistically controlled. However, the MALRT becomes steeper with increasing elevation, leading to lower vertical velocities of isotherm shifts at higher elevations compared with lower elevations (that is, a steeper MALRT corresponds to lower vertical velocities of isotherm shifts). On islands in the Northern Hemisphere, we found higher vertical velocities of isotherm shifts (7.46 ± 2.33 m per year) exceeding, on average, the mean vertical velocity we found across all main continents in the Northern Hemisphere (6.29 ± 2.61 m per year; Fig. 4d,e; df = 3, F = 352.9, P < 0.001). These results suggest that mountain islands in the Northern Hemisphere are even more threatened by the effects of climate change than are mountains on the mainland, and this poses a high threat to island biodiversity given that mountain islands have many endemic species26,27. However, mountain islands in the Southern Hemisphere do not show vertical velocities of isotherm shifts that are as high as those in the Northern Hemisphere (Fig. 4e).
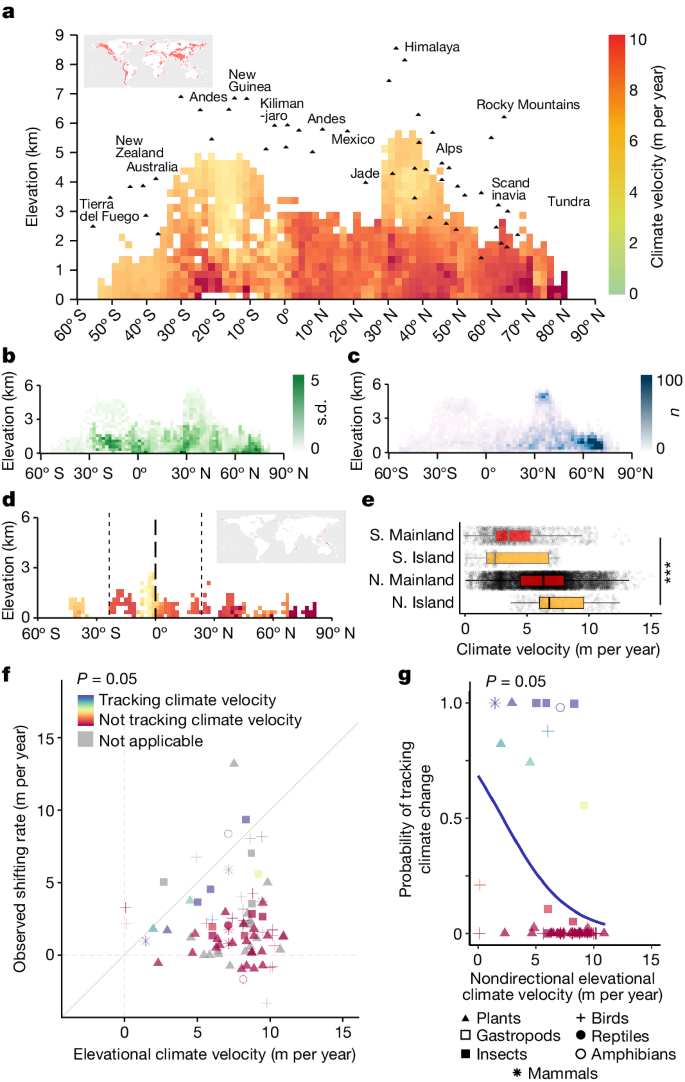
a, Mean climate velocity of mountains worldwide. Mountain summits are labelled for reference. b,c, The corresponding s.d. (b) and sample size (c) for a. d, Mean climate velocity of mountain islands. The s.d. and sample size for d can be found in Supplementary Fig. 3. The colour legend in d is the same as in a. e, The comparison between mainland and islands in the Northern and Southern hemispheres relies on ANOVA and post-hoc Tukey HSD tests. Other than the P = 0.002 between Southern Hemisphere mainland (S. Mainland) and Southern Hemisphere island (S. Island) (by Tukey HSD test), P < 10−16 is shown in all statistics (labelled as ***). The centre line of the box plot represents the median; box limits, upper and lower quartiles; whiskers, 1.5 times the interquartile range. The sample sizes for S. Mainland, S. Island, Northern Hemisphere mainland (N. Mainland) and Northern Hemisphere island (N. Island) are 1,222, 199, 10,331 and 284, respectively. f, Observed species range shifts against the vertical velocities of isotherm shifts. Areas labelled as ‘not applicable’ (in grey) denote instances in which the number of records in a taxonomic group falls below the stipulated minimum (in this case, 30) required to conduct a meaningful statistical comparison to the predicted environmental climate velocities. g, The different probabilities of species tracking climate velocities under a P = 0.05 threshold. Only mean values are shown. Upward and downward shifts are shown together with their absolute values. For results based on different P value thresholds, see Extended Data Fig. 6d,e. A total of 83 taxon–region pairs are plotted. Each plot represents 1 to more than 400 raw data points. See Extended Data Fig. 6b,c for details and Supplementary Fig. 4 for raw data points. All statistics used a two-tailed approach without adjustment for multiple comparisons.
Source Data
Next, we used our estimates of the vertical velocities of isotherm shifts in mountains and linked them to empirical data on the velocities of species range shifts along mountain slopes. We used a carefully curated dataset—BioShifts4—which provides the vertical velocities of species range shifts (in m per year along elevation gradients) per taxonomic unit after standardizing the raw range shift estimates reported by authors in their original studies. Because our analysis shows that the MALRT has a much greater explanatory power for predicting the velocities of species range shifts than does the SLRT (Supplementary Results and Extended Data Fig. 5), we report only on the relationship between the velocities of species range shifts along elevation gradients and the vertical velocities of isotherm shifts in mountains as calculated by the MALRT. Indeed, the Akaike information criterion (AIC) values from our models are 35,887, 37,016 and 51,398 for the MALRT, constant LRT and SLRT, respectively, ranking from best to worst in terms of model fit. This discrepancy between the MALRT and the SLRT is likely to be due to the fact that the satellite (MODIS) data measure the actual land surface temperature, which is influenced by microscale surface properties such as albedo, emissivity, rock type and vegetation cover. Hence, for the SLRT, the calculated lapse rate is characterized by considerable noise. Moreover, the SLRT data are available mainly in cloud-free conditions, which intensify these spatial variations. As a consequence, satellite data present several limitations, and thus have a limited capacity to explain species range shifts compared with insights obtained from theoretical calculations of the MALRT. Comparing the vertical velocities of isotherm shifts based on the MALRT with the observed rates of species range shifts, the probability that a given taxonomic unit tracks the vertical velocities of isotherm movements decreases sharply with increasing absolute velocities of isotherm shifts (Fig. 4f,g). Thus, we found that species seem to track climate change only at lower velocities along the elevational gradients, irrespective of the taxonomic group (Fig. 4g, Extended Data Fig. 6d,e and Extended Data Fig. 7). These results reveal the potentially catastrophic effects of rapid climate change on mountain biodiversity. Although the MALRT will probably undergo changes over time owing to temporal variations in the spatial distribution of temperature and water vapour along elevation gradients, it is important to note that the effects resulting from a shallow MALRT are expected to be worrisome.
Our assessment of mountain climate velocity yields a mechanistic understanding of the variability in mountain climate change globally. The thermodynamic theories of the MALRT, which consider water vapour and latent heat release, suggest that threats to mountain biodiversity can occur in the absence of rapid surface warming. As our range shift analysis shows, species are unlikely to track isotherms quickly enough to match the high velocities at which isotherms are moving along some elevation gradients. Our results suggest that the vertical distance between isotherms in mountains is a crucial factor driving species migration. Likewise, on the basis of thermodynamic theory, colder and drier conditions at higher elevations make temperature lapse rates steeper, which, in turn, leads to a contraction of the vertical distance separating isotherms (that is, isotherm spacing contracts when projected on the vertical axis), generating lower vertical velocities of isotherm shifts. This suggests that in many mountain regions, the vertical shift of isotherms decreases with increasing elevation. From the perspective of isotherms shifting upslope owing to warming, higher elevations will experience a slower rate of isotherm shift, meaning that organisms can reach habitats with suitable temperatures by moving shorter vertical distances. However, a steeper temperature lapse rate also means that the environment changes more rapidly with elevation. Therefore, in the case of mountains with a broader base and narrower peaks28, warming might result in a reduction of habitat area for organisms. Because the shape of a mountain affects the amount of habitat available to organisms28, understanding the velocity of climate change, as well as quantifying the suitable habitat area under warming conditions, will be essential for understanding the effects of climate change on mountain biodiversity.
Moreover, our findings suggest that all taxonomic groups will be similarly affected in their abilities to track isotherms along mountain slopes. Considering that the distance of climate tracking is several orders of magnitude shorter in elevation compared with latitudinal gradients, the moving capability of organisms is less likely to be the key constraint in mountain systems. Mountainous regions, with their complex topography, occupy a relatively smaller proportion of landmasses compared with other terrains in the lowlands28. As described above, the available habitat area for organisms in mountain regions is influenced by the shape of the mountain, and many mountains exhibit a reduction in area with increasing elevation. This, combined with biotic interactions such as interspecific competition29,30, might collectively limit the ability of mountain species to track isotherm shifts in the future. Mountains that we identified as facing high risks under climate change are particularly threatened by biotic attrition17, biotic homogenization31, population extirpation32,33,34 and changing ecosystem properties35. Many of these mountains are located in biodiversity hotspots (for example, Sundaland, Irano-Anatolia, southern Africa, the Mediterranean basin, the Atlantic forest, Mesoamerica, the California Floristic Province and Japan)36,37, reinforcing the need to develop climate-change adaptation strategies for the conservation of mountain biota. Other climatic drivers and mechanisms such as precipitation, snow albedo, radiation flux variability, aerosols and land-use changes can also influence energy balance regimes and further mediate mountain climates5,38,39. Despite many efforts to collect data on species range shifts in mountainous regions, the vast majority of data on species range shifts are still concentrated in Europe and North America4. This also creates uncertainty in assessing the biological effects of climate change at a global extent.
We emphasize that our results are crucial for assessing the vulnerability of mountain regions to climate change globally. By integrating surface temperature and water vapour pressure data with a thermodynamic model, we are able to make effective qualitative comparisons of global lapse rates and identify regions with comparatively higher or lower climate velocities. In particular, this approach enhances the explanatory power of our methodology over other existing methods (such as satellite data analysis) for assessing global species range shifts. However, it is important to recognize that our thermodynamic model still suffers from a low predictive accuracy when compared with field measurements of temperature lapse rates, and we cannot accurately quantify local-scale lapse rates solely on the basis of thermodynamic models. This highlights the need for refined mountain meteorological networks along elevational gradients to improve our holistic understanding of the processes that underlie local temperature lapse rates along mountain slopes. Furthermore, some studies have shown that changes in precipitation patterns can affect the range shifts of mountain species15,40, but historical data on precipitation patterns along mountain slopes are extremely scarce compared with data on temperature lapse rates. For that reason, establishing weather stations that also monitor precipitation patterns along mountain slopes remains key for assessing the large-scale effects of precipitation changes on mountainous organisms. We call for the establishment of networks to monitor climate change and its effects in mountain biodiversity hotspots, especially in mountains that are threatened by high velocities of isotherm shifts, such as those we have identified in our study.
