Natural and previously designed proteins exhibit a wide range of helical geometries with local irregularities, kinks and deviations from linearity16 that make it difficult to achieve the properties illustrated in Fig. 1 that enable simple nanomaterial scaling (beyond the one dimension accessed by varying the number of repeats in a repeat protein or coiled coil). To achieve these properties, we designed a series of new building blocks constructed from ideal α-helices with all helical axes aligned. Restricting helical geometry to ideal straight helices with zero helical twist in principle considerably limits what types of structure could be built, but this is more than compensated by the great simplification of downstream material design, as illustrated below. We construct twistless helix repeat (THR) protein blocks from identical straight α-helices (typically 2–4 helices in each unit); the length of the blocks can be varied simply by varying the number of repeat units. In contrast to existing natural and designed repeat proteins17, THRs are constructed to enable modular nanomaterial design: linear blocks are perfectly straight, allowing nanomaterials to be extended and contracted with no alteration in the angles between the constituent monomers; curve blocks have smoothly curving trajectories that stay in-plane; and turn as well as interaction modules enable placement of two blocks in precise relative orientations with angles appropriate for regular material design.
We blueprint THRs by explicit placement of these straight helix structural elements using an extension of the principles used in coiled-coil and helical bundle design16,18. A first helix a0, part of the zeroth repeat, is placed at the origin and aligned to the z axis. A copy of a0 called a1 is then placed at a new location to set the rigid body transformation between the zeroth and first (and all subsequent) repeat units. After this, any other helices (b0, c0 …) that will be part of the repeating unit are placed as appropriate between a0 and a1 to provide more helices to pack against for stability, and the helices are connected with loops19; repetition of this basic unit then generates backbones with the desired geometries17 (Fig. 1b,c). As the helices are perfectly straight and parallel to the z axis, the overall repeat protein trajectory is fully defined by the following transformation parameters from a0 to a1: the distance of displacement in the x–y plane from helical axis to helical axis (d), the change in displacement in the z axis direction (Δh) and the change in helix phase (Δθ; Fig. 1b). The remaining degrees of freedom for the positions of helices b0, c0 …, which define the internal geometry of the repeat, are extensively sampled, sequences are designed using Rosetta FastDesign or ProteinMPNN19,20, and designs are selected for experimental characterization on the basis of packing and sequence–structure consistency metrics (Methods). We obtained synthetic genes encoding the selected designs, expressed them in Escherichia coli and purified the proteins using nickel–nitrilotriacetic acid immobilized metal affinity chromatography. Designs that were solubly expressed were analysed by size-exclusion chromatography (SEC) to determine oligomerization state, and in the case of assemblies a subset was analysed by negative-stain electron microscopy (ns-EM). Experimental success rates and structural homogeneity for different classes of designs are summarized in Supplementary Figs. 1 and 2 and Supplementary Discussion.
To generate straight, linear THRs, we set Δθ to zero. As illustrated in Fig. 2a,b, this results in perfectly straight repeat proteins in which each repeat unit is translated but not rotated relative to the previous unit. There are two subclasses: setting Δh = 0 generates repeat proteins with each repeat unit simply displaced in the x–y plane (Fig. 2a), whereas setting Δh to a non-zero value generates repeat proteins that also step along the z axis (Fig. 2b). We tested 33 linear THRs (with Δh = 0) with helices either about 20 or about 40 residues in height; 23 of 33 tested designs were solubly expressed, and 13 of 19 designs analysed by SEC were primarily monomeric as designed (Supplementary Figs. 1a,b and 2). Structural characterization of the linear building blocks by X-ray crystallography individually and/or cryogenic EM (cryo-EM) in the context of assemblies (see below) revealed that both the detailed internal structures and the overall straight linear geometry were successfully achieved. The backbone root mean square deviations (RMSDs) between the design models and crystal structures of three 20-residue helix designs (THR1, THR2 and THR3) and two 40-residue helix designs (THR5 and THR6) were 0.8, 0.8, 0.4, 0.6 and 1.3 Å, respectively, and in all five cases the relative rotation of successive repeats is nearly zero (Fig. 2a and Supplementary Fig. 6a). We found that we could not only control Δθ = 0, but also program values of the inter-repeat distance d: the crystal structure of a design with d set to a compact helix packing value of 8.7 Å had a very close value of 8.6–8.8 Å at its central interior (THR3), in contrast to most others designed at 10.0 Å (Supplementary Fig. 6b). For structural validation of blocks with non-zero Δh, the cryo-EM structure of an assembly constructed from such a block (THR4) exhibited a linear stair-stepping structure nearly identical to the design model, (backbone RMSD of 1.0 Å; Fig. 2b and Supplementary Fig. 1a).
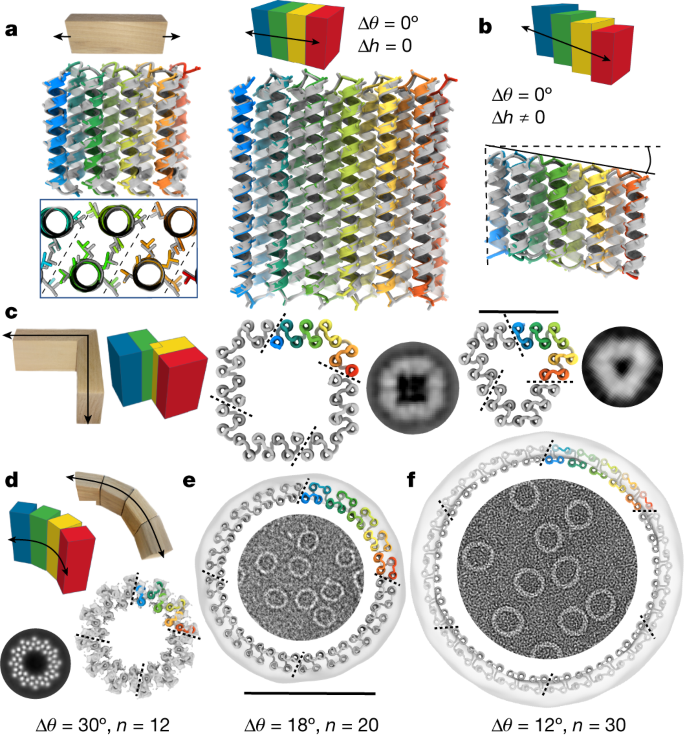
a,b, The linear THR designs (rainbow) are nearly identical to the experimentally determined structures (grey). Side-chain sticks between α-carbon and β-carbon are shown to indicate helical phasing. a, Left: the 2.5-Å-resolution crystal structure of the short, linear THR1 has a 0.8 Å CA RMSD to the design. The inset below shows repeat packing in the THR interior. Right: the 2.7-Å-resolution crystal structure of the tall, linear THR5 has a 0.6 Å CA RMSD to the design. b, Bottom: Comparison of the stair-stepping linear THR4 design model to the cryo-EM structure (determined as part of a nanocage assembly; Supplementary Fig. 16). The CA RMSD between the cryo-EM structure and the design model is 1.0 Å. c, C4 and C3 polygons generated from four-helix turn module THRs as illustrated on the left. C4 square 90_C4_B (middle) and C3 triangle 120_C3_A (right) oligomers with representative ns-EM 2D class averages for comparison (raw EM micrographs are in Supplementary Fig. 1f). Chain breaks are at the ends of the rainbow sections. Scale bar, 4 nm (for the design models); class averages are not to scale. d, Uncapped curve THRs generate cyclic ring oligomers. The 12-repeat ring design (tested as C4) R12B has a cryo-EM 3D reconstruction overlaid on the model; the two are nearly identical. A 2D class average with the individual straight helices resolved is shown left of the ring. e, The 20-repeat ring design (tested as C4) R20A has an ns-EM reconstruction density overlaid on the model, and a raw micrograph is shown inside. Scale bar, 10 nm. f, The 30-repeat ring design (tested as C6) R30A represented in a similar manner to e. Scale bar in e, 10 nm (for the design models with reconstruction maps overlaid in d–f); class averages are not to scale. The asymmetric unit is coloured in rainbow.
To generate turn blocks, we blueprint an additional helix c0 lined up with a0 and a1 that can be assigned any specified phase difference, which can be utilized in fusion operations to produce a turn that is equal to θc − θa (Supplementary Fig. 5d,e). As for all of the THR blocks described here, because of the ideality of the block construction, the same sequence interactions can be used for the intra-block and inter-block interactions; we refer to blocks in which the terminal repeats have identical sequences to the internal repeats as uncapped, and those in which the terminal helices have polar outward-facing residues to prevent self-association (like the linear blocks above) as capped. We experimentally characterized uncapped turn modules that generate rotations of 360/n, in which n is 3, 4, 5 or 6; if the geometry is correct, these should oligomerize to form closed polygons with n subunits. ns-EM 2D class averages of the n = 3 designs clearly show the designed triangular shape with flattened corners (Fig. 2c and Supplementary Fig. 1f), and for n = 4, the designed square shapes (Fig. 2c and Supplementary Fig. 1f) including fine details such as the lower density around the corner helix are observed. For n = 5 and n = 6, success rates were lower, probably because their hinge regions involved less-extensive helix–helix interactions, but we did obtain designs with the expected polygonal structures for both after using reinforced corners on the C6 design (Supplementary Fig. 1f and Supplementary Discussion). Thus, by controlling the phase rotations between adjacent helices, turns can be encoded while maintaining overall parallel helical architecture. We also made polygonal designs with combinations of linear THRs and new straight helix-heterodimer corner junctions instead of turn modules (Supplementary Discussion and Supplementary Figs. 1g, 9 and 10).
To generate curve THRs, we incorporate a phase change (Δθ) between repeating elements (Fig. 1c) that generates a curved trajectory rather than a linear one. We choose Δθ to be a factor of 360° so that perfectly closed rings can be generated. The size of the closed ring can be controlled by specifying Δθ and the distance d between repeats (Supplementary Fig. 7). To access a broad range of d parameter values, we add additional helices to the repeat unit; for circular rings we used four helices per repeat unit. A full curve THR ring with n repeats can be divided into smaller chains each with m repeats, in which m is a factor of n; n/m uncapped repeats can associate to generate the full ring with cyclic symmetry21. To facilitate gene synthesis and protein production, we characterized such split oligomeric versions of the rings rather than synthesizing very long single chains. We designed rings with 12, 18, 20 and 30 repeats ranging from 9 to 22 nm in outside diameter. The 12- and 20-repeat rings were tested as C4 designs, whereas the 18- and 30-repeat rings were tested as C6 designs. Designs for all four ring sizes were remarkably uniform with ns-EM micrographs densely covered with circular assemblies with few to no defects or alternative structures present (Supplementary Fig. 7). Two-dimensional class averages showed that designs for all four sizes were close to the intended size (Fig. 2d; 10, 1 and 9 unique designs yielded distinct ring shapes for 18-, 20- and 30-repeat rings (Supplementary Figs. 1e and 2)). The smallest rings with 12 repeats have solvent-exposed helices exterior to the ring placed to facilitate outward-facing fusions without disrupting the core packing of the ring; these are clearly visible in the 2D class averages and 5.2-Å-resolution cryo-EM reconstruction of R12B (Fig. 2d and Supplementary Fig. 1e) that matches the designed patterning of the helices. ns-EM of the 18-, 20- and 30-repeat rings (with outside diameters of 12, 14 and 22 nm respectively) showed that many designs formed remarkably monodisperse populations of ring-like structures closely consistent with the design models (Fig. 2e,f and Supplementary Fig. 1e). ns-EM class averages of these designs had the smooth and round shape of the design models, and were in most but not all cases homogeneous (some designs assembled into closed-ring species that ranged by ±1 chain of the desired number, resulting in some slightly oblong shapes; Supplementary Fig. 1e). These designs highlight the control over ring curvature that can be achieved by specifying building block repeat rotation parameters.
The simplicity of our blocks in principle enables the reinforcing of designed materials using struts rigidly linking distinct structural elements. As a first test of this, we sought to build concentric ring assemblies from pairs of rings that have different sizes but repeat numbers that share large common denominators. For example, 2 repeat units of a 20-repeat ring can be combined with 3 repeat units of a 30-repeat ring as 10 copies generate a complete ring in both cases (Fig. 3a, left). Rings were segmented into matching cyclic symmetries, the rotation and z displacement of one ring relative to the other was sampled, and linear THRs were placed to connect the inner and outer rings. We constructed single-component C10 concentric ring assemblies by connecting a three-repeat-unit curved block and a two-repeat-unit curved block that both generate a 36° (360°/10) rotation with a radially oriented strut. Two-dimensional class averages of ns-EM images of the designed strutted assemblies show both rings clearly present (Fig. 3a, right; some 11-subunit rings were observed in addition to the target 10-subunit structure). We similarly connected three repeat units with a 20° rotation per repeat, and five repeat units with a 12° rotation per repeat, with a radial strut; the resulting composite subunits map out a 60° rotation of inner and outer rings such that six subunits generate a full 360° ring. The resulting two-component C6 strutted assembly yielded 2D class averages that showed both rings with all chains present, and a 5.1-Å cryo-EM reconstruction was very close to the design model (RMSD 2.7 Å) with very similar outer diameter (19.7 nm versus 20.1 nm; Fig. 3b and Supplementary Fig. 8c). The helix positioning in the inner ring and the strut are also very close to the design model (Supplementary Fig. 8c, insets). Thus, the modularity of the THRs enables designing complex structures by inspection, and enables buttressing to increase structural robustness (Supplementary Discussion and Supplementary Fig. 8).
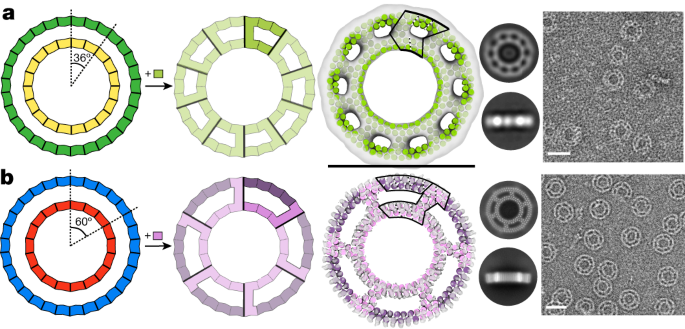
a,b, Two different size rings built from curve THRs for which integral multiples generate the same rotation can be concentrically nested and connected by struts. a, Three repeats of an outer ring (12° per repeat) are combined with two repeats of an inner ring (18° per repeat) that both generate a 36° rotation. Connection of the two pieces with a linear THR generates a C10 single-component ring (strut_C10_8); an asymmetric unit is highlighted in the second ring image. An ns-EM 3D reconstruction in C10 symmetry is shown overlaid with the design model next to 2D class averages and a representative micrograph. b, Five repeats of an outer ring (12° per repeat) are combined with three repeats of an inner ring (20° per repeat) that both generate a 60° rotation. Connection of the two pieces with a linear THR and an additional chain break in the outer ring generates a C6 two-component ring (strut_C6_21); an asymmetric unit is highlighted in the second ring image with the two chains in different colors. A cryo-EM 3D reconstruction in C6 symmetry is shown overlaid with the design model next to cryo-EM 2D class averages and a representative ns-EM micrograph (additional cryo-EM details are provided in Supplementary Fig. 8c). Scale bars, 20 nm (a,b). An asymmetric unit is outlined on top of the design model, and repeats are sectioned with dashed lines.
